Bon, c’est vrai que le chapitre précédent peut sembler complexe. Mais si vous n’avez pas tout saisi, ce ne devrait pas être un problème pour la suite. ;)
Résumons où nous en sommes. Nous avons 2 espaces :
L'espace à p dimensions où l'on a placé le nuage des individus.
L'espace à n dimensions où l'on a placé le nuage des variables.
Pour ces 2 objectifs, nous allons créer 2 graphiques. Chacun d’eux sera à 2 dimensions :
Pour l'objectif 1, ce sera la projection du nuage des individus sur les 2 premiers axes d’inertie, c’est-à-dire sur le premier plan factoriel.
Pour l'objectif 2, ce sera la projection du nuage des variables sur le premier plan factoriel.
Le cercle des corrélations
Dans ce chapitre, nous étudions le second graphique. Il s'appelle le cercle des corrélations.
En voici un exemple :
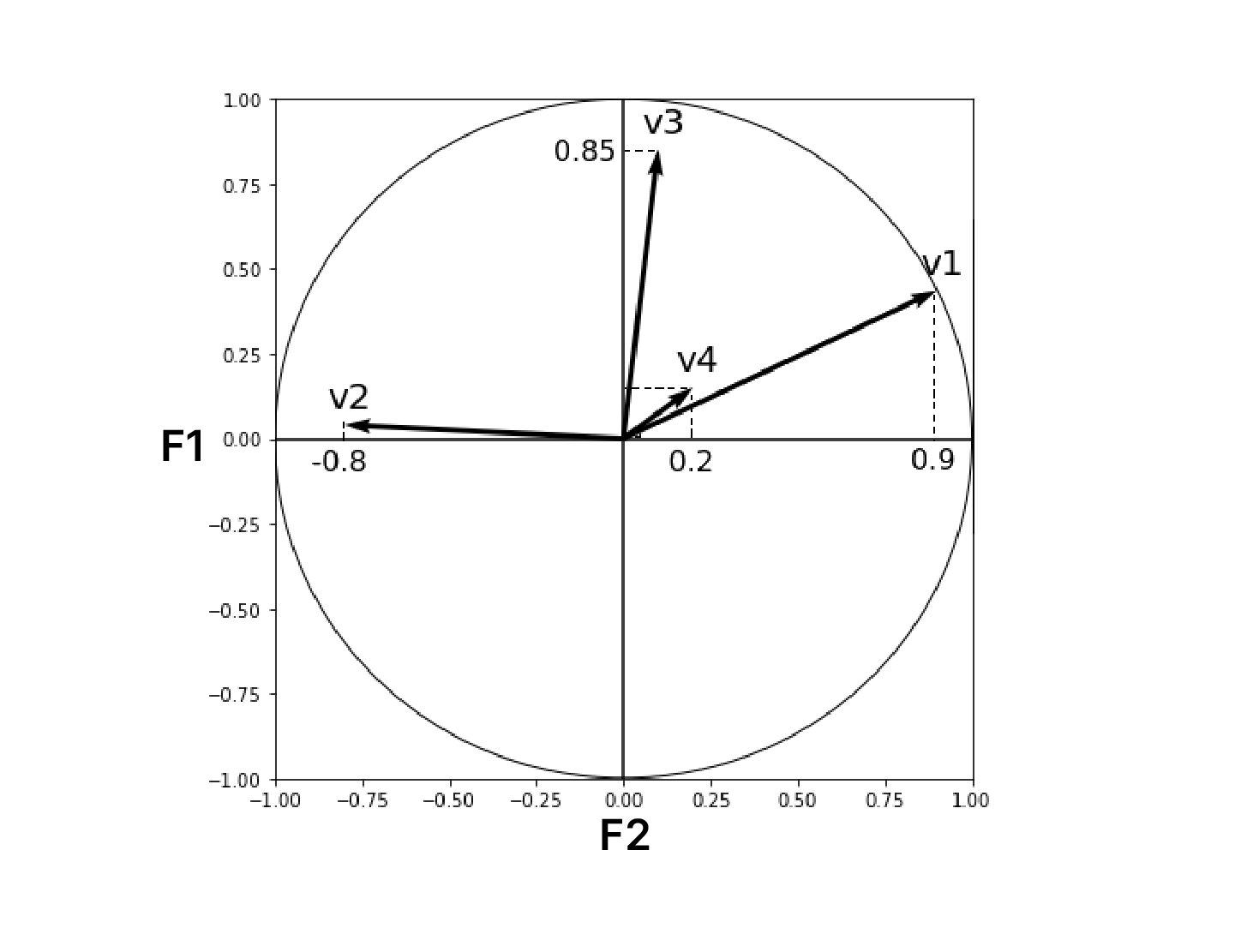
Qu’y voit-on ?
On y voit un cercle, de rayon 1. L’axe des abscisses représente le premier axe d'inertie. L’axe des ordonnées représente .
À l’intérieur du cercle, il y a des flèches qui partent du centre. Elles sont plus ou moins grandes, et peuvent aller jusqu’à toucher le cercle, sans jamais le dépasser.
Comment l’interpréter ?
Rappelons-nous l’objectif numéro 2 : étudier les liaisons entre les variables. On va donc chercher à savoir s’il y a des groupes de variables qui sont fortement corrélées entre elles (deux à deux).
Si de tels groupes existent, alors toutes les variables d’un groupe donné seront « synthétisables » (résumables) par une variable synthétique.
Étudions donc les corrélations entre les variables initiales et les composantes principales !
Mais comment détecter des variables fortement corrélées aux variables synthétiques F1, F2 ?
Il suffit de savoir une chose : la projection de la flèche (représentant la variable ) sur F1 correspond au coefficient de corrélation entre et . Rappelons qu'un coefficient de corrélation est compris entre -1 et 1. Cela tombe bien : le cercle est justement de rayon 1 !
Regardons : sa projection sur F1 vaut 0.9.
Cela signifie que .
De même, on a une variable qui est corrélée négativement à F1 (on dit aussi anticorrélée), c’est-à-dire que, quand croît, alors décroît. Cela se traduit par un coefficient de corrélation proche de -1 (ici -0.8).
Par contre, est très peu corrélée à , mais l’est fortement à . , quant à elle, est très peu corrélée à la fois à F1 et à F2.
Au fait, pourquoi dessiner un cercle ?
On verra un peu plus bas que la longueur des flèches est importante. De plus, cette longueur ne dépasse jamais 1 (avec des données centrées-réduites). Le cercle indique donc la longueur maximale des flèches. Si vous avez bien compris le chapitre précédent, alors lisez la section Allez plus loin, et tout s'éclaircira !
Analyse de votre jeu de données
Pour le jeu de données des cours OpenClassrooms, voici le cercle des corrélations que j'obtiens avec mes données :
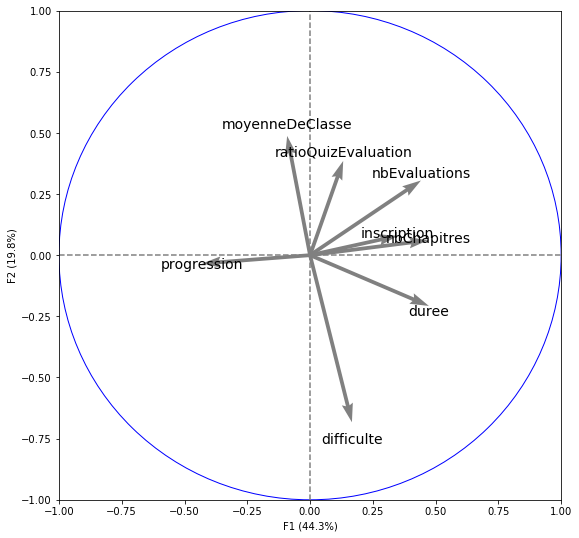
Les variables les plus corrélées à F1 sont :
la durée ;
le nombre de chapitres (nbChapitres) ;
le nombre d’évaluations du cours (nbEvaluations).
Elles sont corrélées positivement à F1, mais on a aussi la variable progression qui est corrélée négativement à F1.
Ce qui est intéressant ici, c’est d’interpréter l’axe F1. Ici, il se trouve que toutes ces variables ont un “mode” commun, c’est-à-dire une notion qui les unit.
Pour les variables durée et nombre de chapitres, c’est évident.
Pour la variable nombre d’évaluations, on comprend facilement que plus un cours est long, plus il a d’évaluations.
La variable progression a une corrélation négative avec F1.
Intuitivement, on comprend que PLUS un cours est long, moins on le finit rapidement, ou moins on a de chances de le finir, d’où la corrélation négative.
Si l'on fait le même travail pour la seconde composante, on voit que les variables les plus corrélées à F2 sont :
la difficulté (avec une corrélation négative) ;
la moyenne de classe ;
la proportion de quiz par rapport au nombre total d’évaluations.
C’est évident pour la variable difficulté, qui lui est anticorrélée.
C’est également compréhensible pour la variable moyenne de classe : plus un cours est facile, meilleures seront les notes des étudiants.
Pour le ratio quiz/évaluation, il faut savoir qu’il y a deux types d’évaluations : les quiz et les activités. Vous avez sûrement remarqué que les quiz sont en général plus simples que les activités. Donc plus la proportion de quiz est importante, plus simple est le cours !
Ça y est, nous approchons de notre objectif : celui de regrouper les variables en variables synthétiques !
En effet, on peut résumer notre jeu de données comme ceci :
Ce qui différencie le plus les cours de notre échantillon, c’est leur longueur. Ensuite, on trouve une deuxième tendance : il y a les cours qui sont faciles, et ceux qui sont difficiles.
Bien entendu, on ne peut pas rendre compte de la complexité de la réalité de nos individus en 2 phrases ! Quand on résume, on perd de l’information, forcément. Cependant, ces 2 phrases sont les 2 phrases « optimales », c’est-à-dire que ce sont celles qui résument le mieux l’échantillon. Si on avait choisi d’autres phrases pour caractériser notre échantillon, alors on aurait perdu plus d’information ; notre résumé aurait été moins bon.
Vous savez que les composantes principales peuvent être vues comme de nouvelles variables, c’est-à-dire comme de nouvelles colonnes de notre tableau de données. Ainsi, on pourrait supprimer toutes les variables initiales et les remplacer par les colonnes F1 et F2.
Bien sûr, on peut aller plus loin et rajouter des phrases à notre résumé, ou des colonnes à notre tableau, en analysant les composantes F3, F4, etc.
Attention aux pièges
Faut-il interpréter les flèches qui sont petites ?
Une flèche qui est petite sur le premier plan factoriel, cela signifie qu’elle est faiblement corrélée à la première composante principale F1, et faiblement corrélée aussi à F2. Mais elle peut très bien l’être à F3, F4, F5, etc.
Ainsi, il est préférable de n’interpréter que les flèches les plus longues, car les flèches les plus petites correspondent à des variables dites « mal représentées » sur le premier plan factoriel.
Mal représentées ?
Oui, c’est encore une histoire de projection. Vous savez que, quand on projette, on perd de l’information. Une variable bien représentée est une variable pour laquelle on perd très peu d’information sur le plan factoriel.
Les variables bien représentées auront une flèche de longueur proche de 1, et leur extrémité sera donc proche du cercle des corrélations. Pour mieux appréhender cette notion, rendez-vous à la section Allez plus loin.
Si certaines variables sont mal représentées, on peut tenter d’afficher le second plan factoriel, avec F3 et F4. On peut aussi continuer avec F5, F6, etc.
Nous verrons prochainement comment bien sélectionner le nombre de plans factoriels à analyser.
Peut-on interpréter les angles entre les flèches ?
Mieux vaut être prudent, et ne pas prendre cette habitude. En effet, le cercle des corrélations n'est pas fait pour interpréter la corrélation entre 2 variables initiales, mais plutôt entre une variable initiale et l'un des axes d'inertie. Pour plus de précisions, descendez cette page jusqu'à la section Allez plus loin.
Variables et angles : qualité de la représentation
Il faut bien garder en tête que les flèches que vous voyez sur le cercle des corrélations sont en fait des projections.
En effet, on a projeté le nuage des variables d'un espace à dimensions vers le plan factoriel, qui est un plan en 2D.
Une flèche, c'est un objet très fin et très long ! Un peu comme un bâton ou une épée.
Prenons cette analogie de l'épée : imaginez-vous au cinéma, en train de regarder un film avec des chevaliers qui se battent à l'épée.
Disons que les épées ont une longueur de 1 mètre.
Sur l’écran de cinéma, la longueur de l’épée apparaîtra maximale si l’acteur la place sur un plan parallèle à l’écran. Mais s’il la déplace et qu’il pointe l’épée directement vers la caméra, alors l’épée vous apparaîtra toute petite, puisqu’elle pointe vers vous.

On peut ainsi dire que, quand la longueur de l’épée est maximale, elle est bien représentée, car vous pouvez appréhender toute sa longueur, alors que, lorsqu’elle pointe vers vous, elle est mal représentée.
Sur le cercle des corrélations, c’est pareil. Une flèche qui est de longueur 1 (et qui touche le cercle) est parfaitement bien représentée : elle est parallèle au plan factoriel. Alors qu’une flèche qui sera parfaitement orthogonale à ce plan aura une longueur de 0.
En pratique
Ce chapitre était déjà assez long et complexe ! Nous verrons la pratique dans le cadre du TP :).
Pour certains d'entre vous, il sera bon de relire ce chapitre après avoir fait le TP. Vous verrez, les choses seront peut-être beaucoup plus claires !
En résumé
Pour analyser le lien entre nos nouvelles dimensions synthétiques et les dimensions originales, on utilise le cercle des corrélations.
Cette étape d'analyse est essentielle.
On y distingue les dimensions qui sont bien représentées des dimensions qui le sont mal : celles qui ont une grande longueur, de celles qui en ont une faible. On le fait sur nos nouvelles dimensions, très souvent F1, F2, et parfois même F3 et F4.
Les nouvelles dimensions dites « synthétiques » sont des combinaisons linéaires des dimensions originales. On peut calculer par exemple F1 = (x * dimension_1) + (y * dimension_2) + (z * dimension_3), etc.
Si deux vecteurs « dimension » ont un angle très proche dans le cercle des corrélations, on aurait envie de déduire que ces dimensions sont fortement corrélées. Mais cette corrélation n'est pas la « vraie » corrélation, c'est celle représentée dans notre nouvel espace F1, F2, par exemple.
Allez plus loin : Que dire des angles entre les variables initiales ?
Au chapitre précédent, nous avons vu que, dans l’espace , on représente les variables par des flèches, et que toutes les flèches ont la même longueur (à condition que les données soient centrées-réduites).
Nous avons vu aussi que, dans , le cosinus de l’angle entre 2 flèches correspond au coefficient de corrélation entre les 2 variables correspondantes. Si 2 flèches sont très proches, l’angle qui les sépare est proche de 0°, et cos(0)=1 , donc leur coefficient de corrélation est proche de 1 : ces 2 variables sont très corrélées. De même, si 2 flèches sont orthogonales (perpendiculaires), alors l’angle qui les sépare est de 90°. Le cosinus de cet angle valant 0, deux flèches orthogonales correspondent à des variables non corrélées (indépendantes).
On ne peut déduire cela QUE si leurs 2 extrémités sont proches du cercle. Si ce n’est pas le cas, c’est parce qu’elles sont mal représentées sur le plan factoriel. Si elles sont mal représentées, alors il ne faut pas les interpréter ni interpréter l’angle qui les sépare.
De même, on peut croire que 2 flèches perpendiculaires correspondent à des variables indépendantes (non corrélées). Là encore, on ne peut déduire cela QUE si ces 2 variables sont bien représentées sur le plan factoriel !
Si cependant vous pensez voir sur le cercle des variables fortement corrélées (ou au contraire non corrélées), alors calculez absolument leurs coefficients de corrélation pour vérifier. Sachez qu'il existe une représentation bien pratique qui donne tous les coefficients de corrélation des variables deux à deux. Elle s’appelle la matrice des corrélations.
Allez plus loin : Pourquoi un cercle ?
Nous avons vu au chapitre précédent que le cercle, la sphère et l'hypersphère étaient de la même famille. En effet, le cercle est composé de tous les points situés à égale distance du centre du cercle, dans un espace à 2 dimensions. La sphère est son équivalent dans un espace en 3D, et l'hypersphère en est l'équivalent pour tout espace de plus de 3 dimensions.
Par exemple, quand vous prenez un compas et que vous réglez l’espacement entre la pointe et la mine sur une longueur de 5 cm, vous tracez un cercle de 5 cm de rayon. Le compas vous aura permis de dessiner tous les points qui sont à 5 cm de là où vous avez planté la pointe du compas.
Ensuite, il faut savoir que la projection d'une sphère ou d'une hypersphère sur un espace en 2D donne un cercle. En effet, quand une caméra filme un ballon de foot, le ballon vous apparaît comme un cercle sur l'écran de cinéma. Mais en réalité, le ballon de foot est une sphère, pas un cercle !
Revenons à notre nuage des variables .
Les extrémités des flèches du nuage des variables sont donc placées sur une hypersphère, car elles sont toutes de même longueur.
Mais comme le graphique du cercle des corrélations est en 2D, on projette cette hypersphère sur le premier plan factoriel. La projection de cette hypersphère sur un plan donne… un cercle ! Ainsi, le cercle des corrélations est simplement la projection de l'hypersphère sur le premier plan factoriel !
Ainsi, le cercle des corrélations est la projection de l’hypersphère sur le plan factoriel ! De même, les variables du nuage des variables sont aussi projetables sur ce plan : leur projection donne les flèches qui sont à l’intérieur du cercle des corrélations.
